
The form of the definition involves a "product moment", that is, the mean (the first moment about the origin) of the product of the mean-adjusted random variables hence the modifier product-moment in the name. Pearson's correlation coefficient is the covariance of the two variables divided by the product of their standard deviations. The naming of the coefficient is thus an example of Stigler's Law.
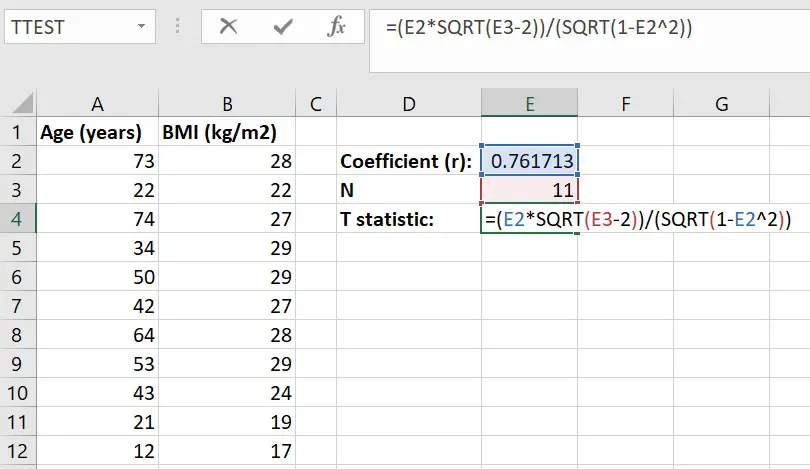
It was developed by Karl Pearson from a related idea introduced by Francis Galton in the 1880s, and for which the mathematical formula was derived and published by Auguste Bravais in 1844. 5.5 Using the exact confidence distribution.5.3 Testing using Student's t-distribution.4.2 Interpretation of the size of a correlation.As a simple example, one would expect the age and height of a sample of teenagers from a high school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation). As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationship or correlation.
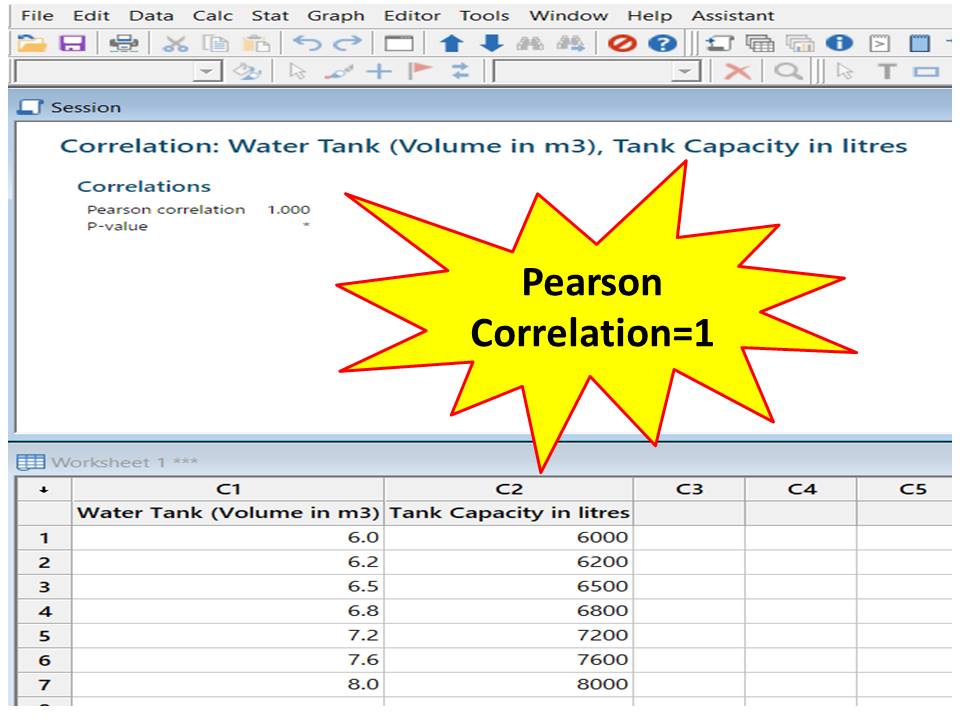
It is the ratio between the covariance of two variables and the product of their standard deviations thus it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. In statistics, the Pearson correlation coefficient ( PCC, pronounced / ˈ p ɪər s ən/) ― also known as Pearson's r, the Pearson product-moment correlation coefficient ( PPMCC), the bivariate correlation, or colloquially simply as the correlation coefficient ― is a measure of linear correlation between two sets of data. For broader coverage of this topic, see Correlation coefficient.


 0 kommentar(er)
0 kommentar(er)
